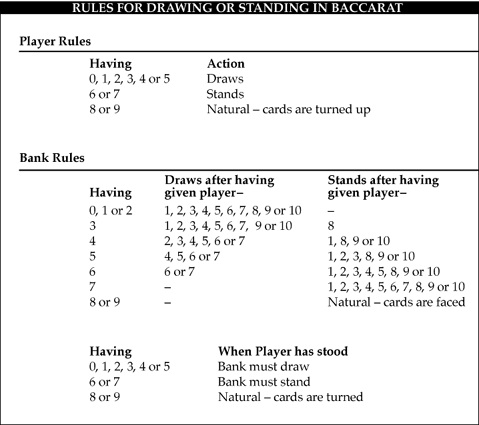
How To Count Cards In Baccarat
The description in the above title is incomplete. It should be:
How Do You Count Cards In Baccarat

How to count cards to exploit third card asymmetrical play to win baccarat in banker bets and tie bets as a standee.
You already know that you can count cards to win in tie games. You can review the post again if you are not aware of the strategy:
Card counting in Baccarat means that the higher or more positive the count is, the more likely it is for the player side to win. If you have a total count of (+5), keep your bet on the player side. Although the banker side winning generally issues a small commission for the casino but playing the tie side is never a good idea since the odds are. The Mechanics of Card Counting Baccarat When there's a new shoe or deck used, you start over with a count of zero. When an ace, two or three is dealt from the deck, you'll add one to that count, which indicates an increased chance of switching to the player bet. Fours are worth double, so you'll add two to the count when these cards are dealt.
If you are counting cards to win in tie bets, why not take advantage of your card count to win in banker bets. This is how I do it.
You rely on symmetrical play and asymmetrical play in baccarat. Revise my post here.
The key points are:
1. In symmetrical play, player has zero odds. The odds for banker is 2.5%.
2. In asymmetrical play, banker has 15.7% advantage over player. After 5% commission, banker advantage is 10.2%.
3. Symmetrical play occurs in 90% of the bets.
Therefore, you exploit asymmetrical play to win in banker bets.
Here is how I do it.
You will notice that symmetrical play occurs in points 0,1,2,7,8,9.
Asymmetrical play occurs when banker two cards show 3,4,5,6.
You will also notice that in this set of numbers 0,1,2,7,8,9, the first three numbers always end up as three cards symmetrical play whereas the last three numbers 7,8,9 always trigger two cards symmetrical play.
You will work out your strategy step by step.
Divide into three groups.
Group A covers points 7, 8, 9
Group B covers points 1 and 2
Group C covers points zero.
The differences in Groups A, B and C are only important in borderline scenarios.
In Group A, your goal is to eliminate points 7, 8, 9 in the outcome.
Scenario 1
When the remaining cards are 10, J, Q, K, 1, single 2 and a single 3, points seven , eight and nine can never be formed. You have eliminated the three essential points. Your advantage to bet banker is 10.2%.
Scenario 2
When the remaining cards are 10, J, Q, K, 1, 2, points seven , eight and nine can never be formed. Bet banker.
How To Count Cards In Blackjack With Multiple Decks
Scenario 3
When the remaining cards are 10, J, Q, K, 1, points seven , eight and nine can never be formed. Only points 0,1,2,3 can form. Bet banker.
Scenario 4
When the remaining cards are 10, J, Q, K, 2, points seven , eight and nine can never be formed. Only points 0,2,4,6 can form. Bet banker.
Scenario 5
When the remaining cards are 10, J, Q, K, 5, points seven , eight and nine can never be formed. Only points 0 and 5 can form. Bet banker.
Scenario 6
When the remaining cards are 10, J, Q, K, and two 6, points seven , eight and nine can never be formed. Only points 0, 2 and 6 can form. Bet banker.
Scenario 7
When the remaining cards are 10, J, Q, K, and many 6, points seven and nine can never be formed. Only points 0, 2, and eight can form. Bet banker three units.
Scenario 8
When the remaining cards are 10, J, Q, K, 6,7, points 1,2, can never be formed. Only points 0, 3, 4,5,6,7,8,9 can form. Bet banker two units.
Scenario 9
When the remaining cards are 10, J, Q, K, 4, 5. Here remember that banker four and five points give you the greatest advantage in asymmetrical play. In this scenario, only points 0, 4, 5, 8, 9 can form. You have eliminated points 1,2,3,6,7. This is a complex scenario. I usually bet only one unit. Banker has only a very slight borderline advantage. Try to figure out yourself. However, it is a good spot for tie bets.
Note: All the nine scenarios are ideal for tie play.
ANALYSIS
There are altogether six numbers for you to eliminate. Here is how I bet. If I am able to eliminate five numbers I bet five units, if four, four units, if three, three units, if two, two units, if one, one unit.
In scenarios 1 to 6, you have eliminated seven, eight and nine, so you always bet three units.
Don’t learn by rote. Learn the method and figure out yourself the bordeline scenarios where you also have some advantage. Keep practising until it becomes second nature to you.
Normally when you have banker advantage is also the time when you have tie advantage , so bet accordingly.
KEY POINTS
1. Counting cards to win baccarat is very effective if you bet both banker and tie bets accordingly.
2. Do not bet player even if you are card counting to win baccarat because player odds at best drop to zero, never positive.
Social Bookmarking
- Appendices
- Baccarat Analysis
- Miscellaneous
Introduction

In either blackjack or baccarat a good first step in developing a card counting strategy is to determine the effect of removing any given card from the game. The following table shows the number of banker, player, and tie wins resulting from the removing of one card in an 8-deck shoe. The card removed is indicated in the image--leftolumn.
Number
| Card Removed | Banker Win | Player Win | Tie Win |
|---|---|---|---|
| 1 | 2259266202814720 | 2198201626637560 | 468838163231312 |
| 2 | 2259390347439480 | 2198279181695870 | 468636463548240 |
| 3 | 2259415336955130 | 2198240411263230 | 468650244465232 |
| 4 | 2259565639560830 | 2198132965463160 | 468607387659600 |
| 5 | 2259056540713470 | 2198626760121850 | 468622691848272 |
| 6 | 2259230629854970 | 2198942636434940 | 468132726393680 |
| 7 | 2259288625471740 | 2198847351781120 | 468170015430736 |
| 8 | 2258880877214840 | 2198299582316670 | 469125533152080 |
| 9 | 2259013211112320 | 2198292198535290 | 469000583035984 |
| 10 | 2259094649086970 | 2198163195365880 | 469048148230736 |
The next table puts these number is some perspective by indicating the probability of a banker, player, and tie win according to the card removed.
Probability
| Card Removed | Banker Win | Player Win | Tie Win |
|---|---|---|---|
| 1 | 0.458613 | 0.446217 | 0.09517 |
| 2 | 0.458638 | 0.446233 | 0.095129 |
| 3 | 0.458643 | 0.446225 | 0.095132 |
| 4 | 0.458673 | 0.446203 | 0.095123 |
| 5 | 0.45857 | 0.446303 | 0.095127 |
| 6 | 0.458605 | 0.446367 | 0.095027 |
| 7 | 0.458617 | 0.446348 | 0.095035 |
| 8 | 0.458534 | 0.446237 | 0.095229 |
| 9 | 0.458561 | 0.446235 | 0.095203 |
| 10 | 0.458578 | 0.446209 | 0.095213 |
The next table shows the house edge of each bet by card removed.
House Edge
| Card Removed | Banker | Player | Tie |
|---|---|---|---|
| 1 | 0.010535 | 0.012396 | 0.143467 |
| 2 | 0.010527 | 0.012405 | 0.143836 |
| 3 | 0.010514 | 0.012418 | 0.14381 |
| 4 | 0.010463 | 0.01247 | 0.143889 |
| 5 | 0.010662 | 0.012267 | 0.143861 |
| 6 | 0.010692 | 0.012238 | 0.144756 |
| 7 | 0.010662 | 0.012269 | 0.144688 |
| 8 | 0.010629 | 0.012298 | 0.142942 |
| 9 | 0.010602 | 0.012326 | 0.14317 |
| 10 | 0.01056 | 0.012369 | 0.143083 |
The next table shows the effect on the house edge of each bet according to the card removed. A negative number indicates removal is bad for the player, positive indicates removal is good.
House Edge
| Card Removed | Banker | Player | Tie |
|---|---|---|---|
| 0 | 0.000019 | -0.000018 | 0.000513 |
| 1 | 0.000044 | -0.000045 | 0.000129 |
| 2 | 0.000052 | -0.000054 | -0.000239 |
| 3 | 0.000065 | -0.000067 | -0.000214 |
| 4 | 0.000116 | -0.000120 | -0.000292 |
| 5 | -0.000083 | 0.000084 | -0.000264 |
| 6 | -0.000113 | 0.000113 | -0.001160 |
| 7 | -0.000083 | 0.000082 | -0.001091 |
| 8 | -0.00005 | 0.000053 | 0.000654 |
| 9 | -0.000023 | 0.000025 | 0.000426 |

The next table multiplies the above numbers by ten million.
Count Adjustment
| Card Removed | Banker | Player | Tie |
|---|---|---|---|
| 0 | 188 | -178 | 5129 |
| 1 | 440 | -448 | 1293 |
| 2 | 522 | -543 | -2392 |
| 3 | 649 | -672 | -2141 |
| 4 | 1157 | -1195 | -2924 |
| 5 | -827 | 841 | -2644 |
| 6 | -1132 | 1128 | -11595 |
| 7 | -827 | 817 | -10914 |
| 8 | -502 | 533 | 6543 |
| 9 | -231 | 249 | 4260 |
| Average | 0 | 0 | 0 |

To adapt this information to a card counting strategy, the player should start with three running counts of zero. As each card is seen as it leaves the shoe the player should add the point values of that card to each running count. For example if the first card to be played is an 8 then the three running counts would be: banker=-502, player=533, tie=6543. Of course the player does not have to keep a running track of all three counts. In fact the point values for the banker and player are nearly opposite of each other. A high running count for the banker would mean a corresponding low count for the player, and vise versa.
In order for any given bet to become advantageous the player should divide the running count by the ratio of cards left in the deck to get the true count. A bet hits zero house edge at the following true counts:
- Banker: 105791
- Player: 123508
- Tie: 1435963
Assuming you were able to actually play this strategy perfectly you would notice that the true counts seldom passed the point of zero house edge. The next table shows the ratio of hands played, based on a sample of 100 million, in which the true count passes the break even points above. The image--leftolumn indicates the ratio of cards dealt before the cards are shuffled.
Positive Expectation
| Penetration | Banker | Player | Tie |
|---|---|---|---|
| 90 percent | 0.000131 | 0.000024 | 0.000002 |
| 95 percent | 0.001062 | 0.000381 | 0.000092 |
| 98 percent | 0.005876 | 0.003700 | 0.002106 |
The final table indicates the expected revenue per 100 bets and a $1000 wager every time a positive expected value occured. Please remember that this table assumes the player is able to keep a perfect count and the casino is not going to mind the player only making a bet once every 475 hands of less.
Expected Profit
| Penetration | Banker | Player | Tie |
|---|---|---|---|
| 90 percent | $0.01 | $0.00 | $0.00 |
| 95 percent | $0.20 | $0.06 | $0.15 |
| 98 percent | $2.94 | $1.77 | $11.93 |
I hope this section shows that for all practical purposes baccarat is not a countable game. For more information on a similar experiment I would recomment The Theory of Blackjack by Peter A. Griffin. Although the book is mainly devoted to blackjack he has part of a chapter titled 'Can Baccarat Be Beaten?' on pages 216 to 223. Griffin concludes by saying that even in Atlantic City, with a more liberal shuffle point than Las Vegas, the player betting $1000 in positive expectation hands can expect to profit 70 cents an hour.
For your further consideration I would recommend this baccarat odds calculator. You can put in any deck composition and it will give the house edge on all three bets.
Go back to baccarat
Go to baccarat appendix 1
Go to baccarat appendix 3
Go to baccarat appendix 4
Go to baccarat appendix 5
Go to baccarat appendix 6
Go to baccarat appendix 7
Written by: Michael Shackleford